转自:https://www.cnblogs.com/FZfangzheng/p/8529132.html
深度优先搜索DFS和广度优先搜索BFS简单解析
与树的遍历类似,图的遍历要求从某一点出发,每个点仅被访问一次,这个过程就是图的遍历。图的遍历常用的有深度优先搜索和广度优先搜索,这两者对于有向图和无向图均适用。
一.深度优先搜索
1.理解分析
首先,让我们来看一看更些简单的深度优先搜索DFS。顾名思义,这个搜索方法是以深度优先,也就是先一条路走到黑,撞到南墙再回头。我们可以看做是一棵树,优先走到根部,然后换一根继续走到最后。下面给出一张图便于理解。
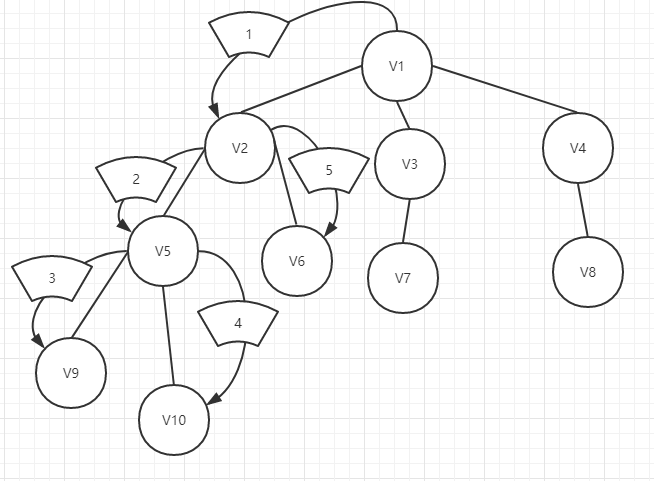
我们可以看到,我们先从V1出发前往V2,然后继续往更深的地方出发,前往V5,V9,然后由于V9是根的最深处,于是我们返回上一层(V5所在),发现还有一个V10没有搜索,所以我们前往V10,然后由于V10是最深的地方,接着往回上一层(V5所在),看看是否还有没有访问搜索的点,发现没有,接着返回上一层(V2所在),发现还有一个V6没有访问,于是搜索访问V6。如此重复,这样就是深度优先搜索。
我们来仔细思考下这个过程,有没有发现和递归有着类似之处?
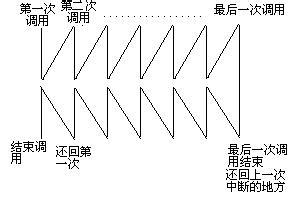
我们来看一看,第一次调用,我们可以理解为目前处于第二层搜索V2节点,第二次调用,我们可以理解为DFS里搜索该节点下的第三层节点,调用完成后结束调用可以看做返回第一层,这样,其中一条V2及以下都已经被遍历过,重复过程,改变参数,我们可以使得所有都被遍历过一次。所以,我们一般采用递归的方法来实现DFS。
2.例题分析
油田问题可以说是经典的使用DFS解决的问题了。
Input:
Output:
2输入的第一行是油田行数和列数,@符号代表油田,我们要求的是的 @ 符号连成一块地(横竖斜相连都算),能有几块这样的油田地。下面给出代码:#include#include #include #include using namespace std; int map[150][150];//用来记录该地是否被查询过,0代表没有 int x, y; char p[150][150];//存放油田 int find(int a, int m, int n) { if (map[m][n] != 0|| p[m][n] != '@')//当不是油田(也就是搜索到头了),并且被找过了,则返回0 return 0; else { map[m][n] = a; //下面这些就是递归部分,写成这样分开便于理解 //先一直往横坐标加1,往右侧不断查询,以下同理 find(a, m + 1, n); find(a, m + 1, n + 1); find(a, m + 1, n - 1); find(a, m, n + 1); find(a, m, n - 1); find(a, m - 1, n + 1); find(a, m - 1, n); find(a, m - 1, n - 1); } return 0; } int oilPocket(int a) { int i, j; for (i = 0; i < x; i++) { for (j = 0; j < y; j++) { if (map[i][j] == 0 && p[i][j] == '@') { //当遇到一块油田没有被遍历过,则以这个点进行深度优先搜索 find(a, i, j);//a代表这块大油田地是第几块,ij就是坐标 a++; } } } return a; } int main() { int ans; while (scanf("%d %d", &x, &y) != EOF) { if (x == 0 || y == 0) break; memset(p, '*', sizeof(p)); for (int i = 0; i < x; i++) { cin.get();//存回车 for (int j = 0; j < y; j++) { scanf("%c", &p[i][j]); } } memset(map, 0, sizeof(map)); ans = oilPocket(1) - 1; printf("%d\n", ans); } return 0; }
这段代码主要是find函数部分,我们可以看到,每次递归都是一开始往右侧找,找到头后往下找,每次都是有着固定的方向,一路寻找到头,然后才会改变方向。这样,我们就使用DFS成功地求得连接在一起的油田数量。
- 有一点在写深度优先搜索时容易犯错误,那就是注意要判断该点是否查询过,反复查询会导致无限递归从而程序出现错误。
二.广度优先搜索
1.理解分析
和深度优先搜索不同的是,我们先访问的是同一层未被搜索过的点,当该层搜索完毕后,我们才会往下一层进发,开始下一层的搜索。
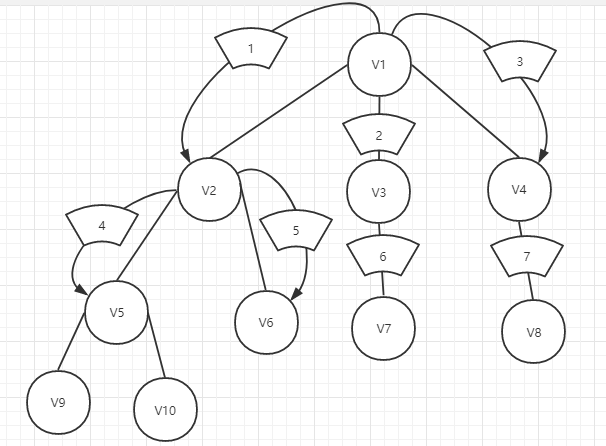
由图我们可以看到我们从V1开始,选择搜索V2,接下来并没有同深度优先搜索一样,搜索V5,而是接着看看同层是否有未被搜索过的点,我们发现V3没有被搜索过,所以我们接着搜索V3,知道V3,V4都被搜索过,我们才开始往下一层进发,搜索V5,V6......
接着,我们来仔细想想,我们该怎么实现BFS呢?
我们发现,如果我们把同一层的点存起来,那么,先进先出的话,同层点在被访问过后,才会接着访问下一层的点。而先进先出正是队列的特点,所以,我们可以使用队列来实现BFS。
2.例题分析
奇怪的电梯,可以使用BFS来解决,当然也可以使用DFS和Dijkstra
来解决(有兴趣可以尝试下)奇怪的电梯题目输入是当前所在楼层,目的楼层,楼层总数,每层电梯只能上下的层数。
输出是最少的次数,不能到达则-1。#include#include #include using namespace std; queue q; int num,s,e; int a[1000]; int step[1000]; void bfs(){ int m,n; while(!q.empty()) { m = q.front();//取出当前队列第一个数,即当前楼层 q.pop(); n = m + a[m];//往上移动到的楼层数 if(n >= 1 && n <= num && step[n] == -1) { step[n] = step[m] + 1;//步数自增 q.push(n);//把当前(移动后的)楼层数加入队列 } n = m - a[m];//往下移动到的楼层数 if(n >= 1 && n <= num && step[n] == -1) { step[n] = step[m] + 1;//步数自增 q.push(n);//把当前(移动后的)楼层数加入队列 } } //队列为空,则表示没有可以移动的位置了,即所有能走的楼层均走过 cout << step[e] << endl; } int main(){ while(scanf("%d",&num)!= EOF) { if(num == 0) { break; } scanf("%d%d",&s,&e);//开始结束楼层 for(int i = 1 ; i <= num ; i++) { scanf("%d",&a[i]);//每层固定上下移动的层数 } memset(step,-1,sizeof(step)); step[s] = 0; q.push(s);//将开始层数加入队列 bfs(); } return 0; }
BFS对于求无权路的最短路径很方便,遍历一遍,到了对应的节点,则可以说是最短路径,对于有权图可以采用Dijkstra等等。
三.总结
BFS和DFS主要是一种遍历图的方式,理解透彻具体是什么,该怎么遍历,熟练之后便可以很快上手,那么该怎么熟练呢?当然是理解+刷题(笑。再来推荐道题目 ,DFS,BFS都可以尝试下(逃